Our research is focused on several aspects of theoretical and computational phylogenetics. Here we list the main directions, but see the publications for more details.
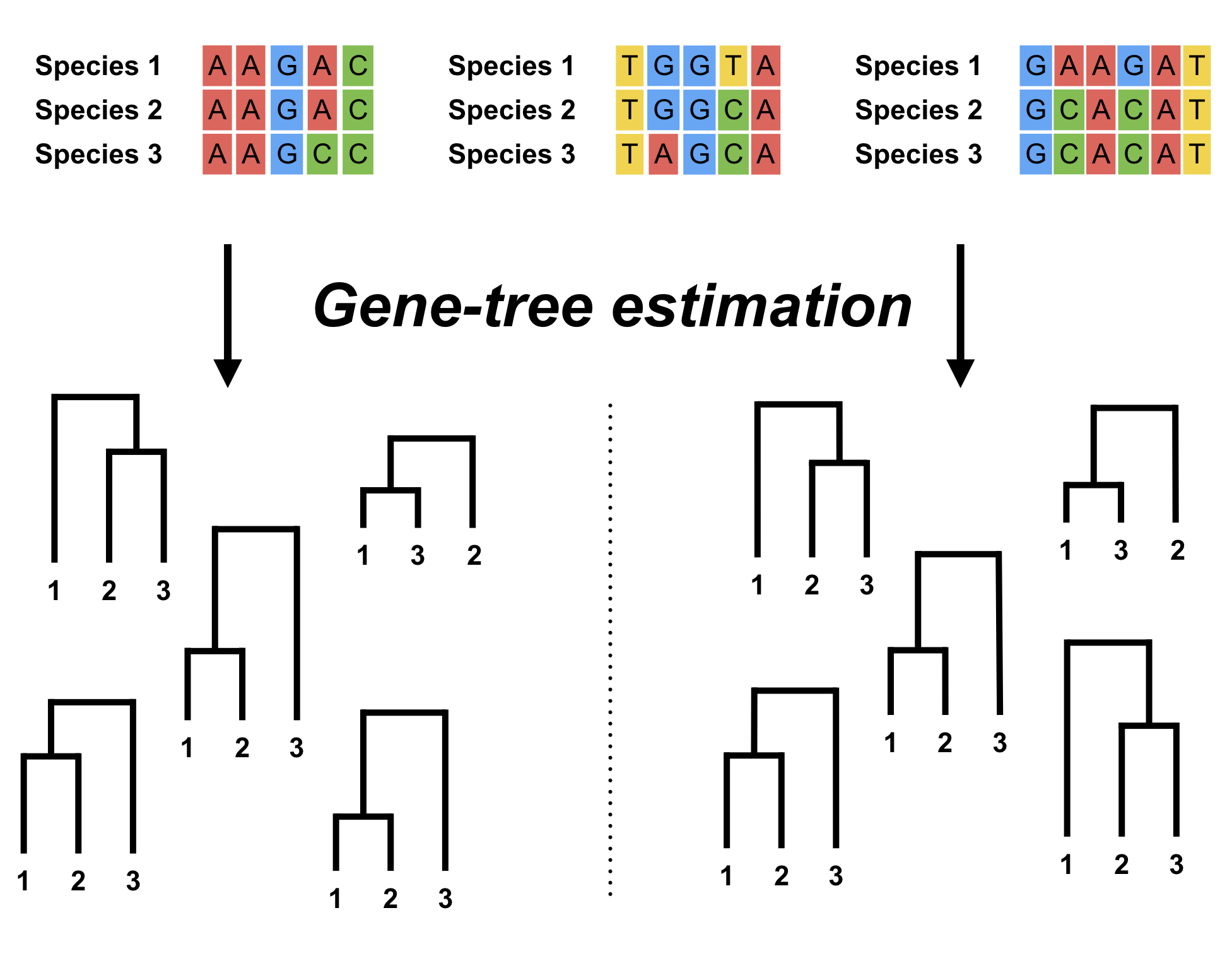
Robust Estimation of Gene Trees
Gene trees provide fundamental information about the processes in genetic evolution which is contained in the variation of their topology and branching times. In this work we are focused on how to reliably estimate gene trees by developing more robust statistical methods.

Understanding Discordance Between Species Trees and Gene Trees
The following biological scenarios can cause incongruent gene trees: (a) simple population genetic processes (i.e., the coalescent), (b) migration and thus gene-flow between species/populations , and (c) gene-duplication and gene-loss. We are working on more realistic models that incorporate different causes of gene-tree incongruence such as the multispecies coalescent with migration model. This work also entails new algorithm development and theory design for more efficient computation of species trees from thousands of gene trees.
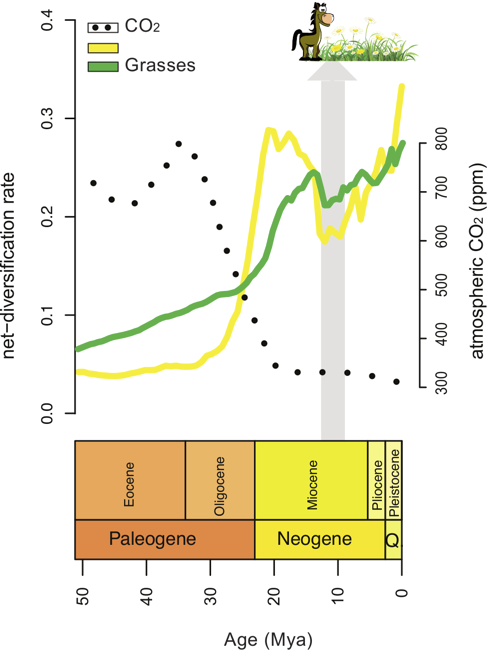
Inference of Macroevolutionary Processes
Our ultimate goal is to infer diversification rates through time and among lineages and identify correlations to genetic, phenotypic and/or environmental factors that impact diversification rate. For example, we developed a statistical method to identify correlations between rates of diversification and environmental variables, such as changes in atmospheric CO2. In our future work, we want to incorporate fossil occurrence information in our models of lineage diversification.